Note from the editor: This is the last of the two-part article series on how real world problems can be solved using fuzzy logic. Part I of this article can be found here.
Fuzzy logic brings in a solution
The brilliant intellectual Lotfi Zadeh introduced Fuzzy Logic in 1973, which constitutes a beautiful solution to problems like the one articulated above. Fuzzy Logic, in its core, builds a sophisticated mathematical framework that can translate semantics expressed in vague human terms into crisp numeric form. This enables us, humans, to express our knowledge in a particular domain using a language familiar to us, but still make that knowledge solve concrete numeric problems. For example, our knowledge can be expressed like the following rules that are used to determine whether a candidate should be chosen for a job depending on his experience, education and salary expectation levels.
- If Experience is High, Education level is Medium and Salary expectation is Low, then hire the guy.
- If Experience is Medium, Education level is High and Salary expectation is High then do not hire the guy.
- If Experience is High, Education level is Somewhat High and Salary Expectation is Very High then do not hire the guy.
Rules like above can be formed using our knowledge, experience, gut feeling, etc about the domain. The collection of rules is typically termed Fuzzy Rulebase. We feed the rulebase into a Fuzzy Logic System (FLS), which aggregates and stores this knowledge. Most notably, the FLS stores the knowledge in a numerical logic that can be processed by a computer. After that FLS is capable of answering questions like the following.
If the Experience level is 4 (out of 5), Education level is 3 and Salary Expectation is 4, should we hire the guy?
No need to mention that, the richer the rulebase is, the more accurate is the outcome.

Lotfi Zadeh
A Little further insight into Fuzzy Logic
How does Zadeh’s new logic perform its wonders under the hood? If fuzzy logic is a complex and amazing structure, the magic brick it is built by is the concept termed possibility. Zadeh’s genius is to identify that, in human discourse, likeliness does not refer to likelihood, but to membership. Let me exercise my teaching guts to describe this in a more digestible form. When we humans are confronted with a question like “How hot is 25oC?” we do not think it like “What is the likelihood that 25oC can be considered hot?” (Do we?). We rather think it like “Up to which degree does 25oC belong to the notion ‘hot’?”. To put the same thing in different terms, it’s about “the degree of belongingness to something” but not ”the probability of being something”. You might now be thinking of giving up the idea of becoming Zadeh’s follower, but I suggest you to hold on and give it a second thought.
I believe that Zadeh touches the real nerve in the problem when he makes this distinction between likelihood and membership. After understanding this by heart it’s an easy ride into the rest of the theory. As the next step we can introduce a term for concepts like ‘hot’, ‘beautiful’ or ‘high’. Fuzzy logic calls them fuzzy sets. A fuzzy set is an association between a number and a possibility value (Possibility is a number between 0 and 1 – just like probability, but at the same time radically deviating from it conceptually).

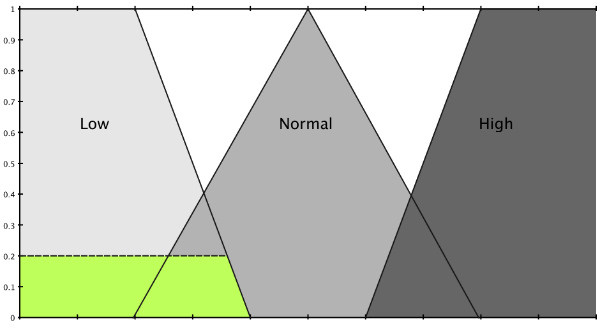
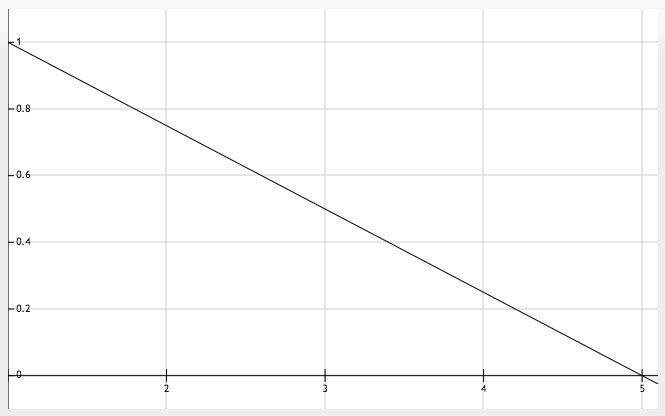
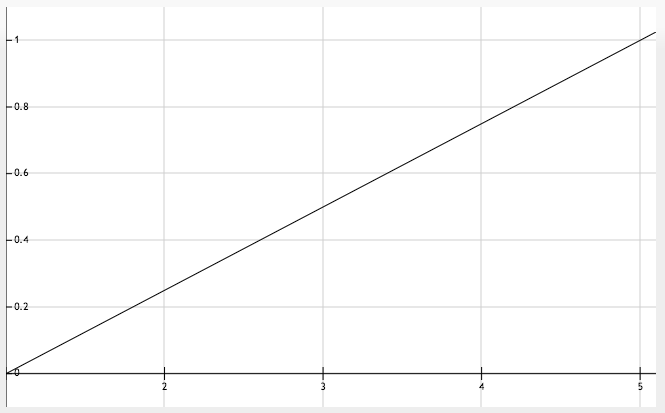
Following figures provide examples. First one defines the fuzzy set “LOW” when input values are given from 1 to 5. For instance, if an examiner evaluates a student’s proficiency in a subject with a number between 1 and 5, how much will each mark mean to be ‘LOW’? We know that 1 is absolutely low. Therefore we consider the possibility of mark 1 being in the fuzzy set ‘LOW’ as 1.0 (maximum possibility). Also we can agree that mark 5 cannot be considered ‘LOW’ at all. So its possibility of being ‘LOW’ is zero. Marks between these two have varying degrees of membership in the fuzzy set ‘LOW’. For example, if the examiner gives mark 4 we consider student’s proficiency to be ‘LOW’ only with a degree of 0.25.
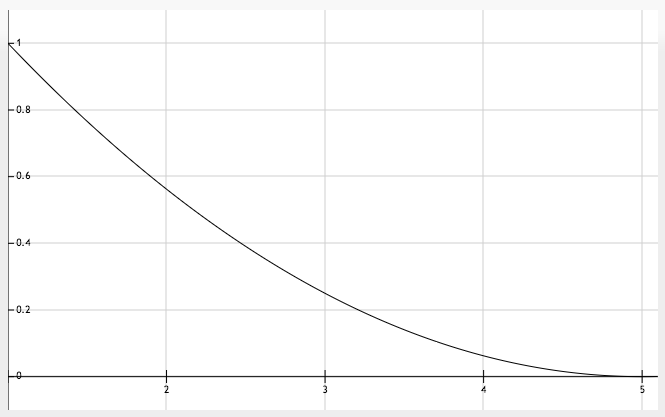
The fuzzy set ‘HIGH’ (last plot) is defined in a similar way. What about the middle one though? It’s not a fuzzy set that stands for a brand new concept, but one that stands for a modification of a previously defined concept. The modifier ‘VERY’ is applied to the concept ‘LOW’. Noting that the modifier is an intensifying modifier (one that further strengthens the concept) we square each possibility in ‘LOW’ to get possibilities in ‘VERY LOW’. Gut feeling says that membership of mark 4 in fuzzy set ‘VERY LOW’ should be less than its membership in ‘LOW’. And the numbers resemble that notion.
- Possibility [4 is VERY LOW] = 0.25 * 0.25 = 0.0625
It’s not difficult to grasp the idea of fuzzy variables. They are fundamentally measurements or entities that can take fuzzy sets as their values. Example fuzzy variables can be temperature, student’s proficiency, candidate’s experience and so on. After that we can combine a fuzzy variable with a fuzzy set to construct a meaningful statement like “temperature is LOW”. These can be termed atomic statements. To express it formally, an atomic statement is of the form:
- <fuzzy variable> is <fuzzy set>
Now we walk the next step by combining several atomic statements into a compound statement. A compound statement would look something like “Student’s math proficiency is LOW, English proficiency is HIGH and music proficiency is MEDIUM”. These types of statements are useful when making judgments based on a combination of factors. For instance, a judge panel might want to make a final decision on whether to pass a student from the exam by looking at all his subject level proficiencies. Suppose that the judge panel decides this: “If there is a student whose math proficiency is MEDIUM, english proficiency is MORE OR LESS LOW and music proficiency is HIGH we will pass him”. This is termed a fuzzy rule. More appropriately, a fuzzy rule is a compound statement followed by an action. Another rule can be: “If the student’s math proficiency is VERY LOW, English proficiency is high and music proficiency is LOW we will fail him”.
If the judge panel can compile a bunch of rules of this form it can be considered to be the policy when evaluating students. In fuzzy logic vocabulary we call it a fuzzy rulebase. It is important to note that a fuzzy rulebase need not be exhaustive (meaning that it does not have to cover all possible combinations of scenarios). It is sufficient to come up with a rulebase that covers the problem domain to a satisfactory level. Once the rulebase is fed to a fuzzy logic system it is capable of answering questions such as “If the student’s math grade is 3 (in a scale of 1 to 5), English grade is 2 and music grade is 3, should we pass him?”. This is all one needs to understand to use a fuzzy logic library. Inner workings of the theory on how it really derives the answer based on rulebase are beyond the scope of a blog post. Also I think that 90% of readers would be happy to learn that the math bullshit is going to end from here.
Application of fuzzy logic into our location detection problem
Let me repeat our problem; we receive location coordinates in iPad with varying frequencies and tolerance levels. By looking at tolerance values and location coordinate frequency, we need to determine whether the device is in high accuracy or low accuracy location detection mode at a given time. We decided to determine the location detection mode every 30 seconds. At each 30 second boundary we used location coordinate values received within the last 30 seconds to determine the mode. All location related processing for the next 30 seconds are performed with respect to this newly figured out mode. For instance, if we decide that the device is operating in high accuracy location detection mode, we assume that the device operates in the same mode until we perform the evaluation after another 30 seconds. For this, we used following two parameters as inputs in the problem.
- Tolerance values for best two location coordinates (coordinates with lowest tolerance values) within past 30 seconds
- Number of location coordinate values received within past 30 seconds (highest possible value is 30 as we configure the device to receive location coordinates every second. However, when in low accuracy mode, number of coordinates received within 30 seconds is way less than 30).
We defined each of the 3 inputs to take values within a universe with 5 fuzzy sets: VERY LOW (VL), LOW (L), MEDIUM (M), HIGH (H) & VERY HIGH (VH). Then we worked out a bunch of fuzzy rules using these inputs and fuzzy sets. Rules are derived using gut feeling decisions on the domain. Following figure shows a part of the rulebase we constructed.
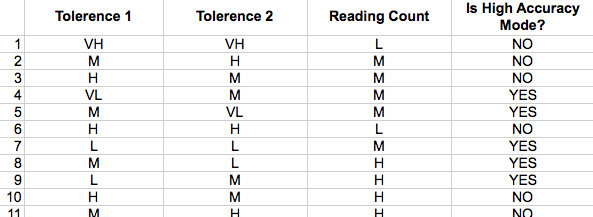
We defined each of the 3 inputs to take values within a universe with 5 fuzzy sets: VERY LOW (VL), LOW (L), MEDIUM (M), HIGH (H) & VERY HIGH (VH). Then we worked out a bunch of fuzzy rules using these inputs and fuzzy sets. Rules are derived using gut feeling decisions on the domain. Following figure shows a part of the rulebase we constructed.
At run time we determine numerical values of our 3 input parameters. An example input set can be:
- tolerence1 = 10 meters, tolerence2 = 25 meters, reading count = 20
Using the rulebase, fuzzy logic system is capable of deriving an answer to the question “Which location detection mode the device is currently operating in?”. Our experimental results were exciting. With the aid of fuzzy logic we arrived at a sensible solution that provides accurate results to a problem that is almost unsolvable using conventional crisp logic. Our app is now in AppStore as the most popular navigation app in Norwegian market.